Разбор задачи A10 (демо ЕГЭ 2013)
( (x ∈ А) → (x ∈ P) ) \/ (x ∈ Q)
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
- [0, 3]
- [3, 11]
- [11, 15]
- [15, 17]
Нужно решить уравнение: ( (x ∈ А) → (x ∈ P) ) \/ (x ∈ Q)=1.
1 способ
Будем решать методом от противного. Пусть ( (x ∈ А) → (x ∈ P) ) \/ (x ∈ Q)=0.
Преобразуем данное уравнение в систему уравнений:
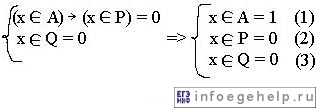
Отрезки P и Q нам заданы, изобразим их:
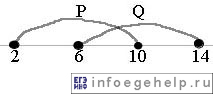
Mы можем решить уравнения (2) и (3) в системе. x∈P=0 => x∉P. Аналогично, x∉Q.
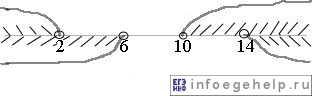
Получили интервал: (−∞;2)υ[14;+∞).
Мы решали методом от противного, поэтому инвертируем полученный интервал: [2;14].
Рассмотрим предложенные варианты:
[0, 3] - не подходит;
[3, 11] - подходит, т.к. [3, 11] включен в [2;14];
[11, 15] - не подходит;
[15, 17] - не подходит;
Получили, А∈[3; 11]
2 способ
Решим уравнение: ( (x ∈ А) → (x ∈ P) ) \/ (x ∈ Q)=1 методом подстановки.
В уравнение вместо P, Q впишем сами отрезки: [2, 10] и [6, 14].
(x ∈ А)=1 для всех вариантов.
| Вариант ответа | Интервал A | Значения x для проверки (границы интервала) | ((x ∈ А) → (x ∈ [2, 10]) ) \/ (x ∈ [6, 14]) |
|---|---|---|---|
| 1 | [0, 3] | 0, 3 | (1→0)V0=0 (1→1)V0=1 |
| 2 | [3, 11] | 3, 11 | 1 (1→0)V1=1 |
| 3 | [11, 15] | 11, 15 | 1 (1→0)V0=0 |
| 4 | [15, 17] | 15, 17 | 0 (1→0)V0=0 |
В таблице розовым выделен искомый интервал.








