Разбор задачи A20 (демо ЕГЭ 2008)
| вверх | вниз | влево | вправо |
При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
| сверху свободно | снизу свободно | слева свободно | справа свободно |
Цикл ПОКА < условие > команда
выполняется, пока условие истинно, иначе происходит переход на следующую строку.
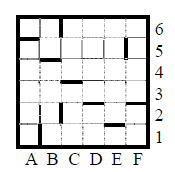
Сколько клеток лабиринта соответствуют требованию, что, выполнив предложенную программу, РОБОТ остановится в той же клетке, с которой он начал движение?
НАЧАЛО
ПОКА < справа свободно > вправо
ПОКА < сверху свободно > вверх
ПОКА < слева свободно > влево
ПОКА < снизу свободно > вниз
КОНЕЦ
- 1
- 0
- 3
- 4
Сначала построим траекторию движения робота. Она изображена на рисунке:
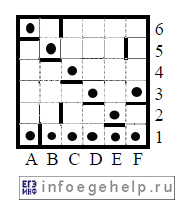
Черной точкой обозначена клетка, из которой начнет движение робот. Из рисунка видно,что клетка, из которой должен начать движение робот, должна быть снизу ограничена барьером. Стена, окружающая лабиринт, также является барьером. Если это условие не будет выполняться, то робот пройдет дальше и не остановится в клетке, с которой начал движение. Отметим клетки,ограниченные снизу барьером. Это и будут потенциальные клетки,которые нам нужно найти.
Теперь проверим каждую из этих точек. Для каждой точки нарисуем траекторию движения робота.
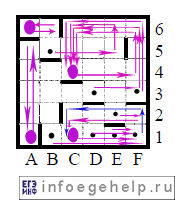
Из точки F1 траектория дальнейшего движения робота для точек B1, C1, D1, E1 и F1 одинакова,поэтому нарисована 1раз сразу для всех точек (чтобы рисунок был нагляднее). Данная траектория изображена синим цветом.
Только четыре клетки (вариант 4) удовлетворяют требованиям задачи: робот вернется в ту же клетку, с которой начал движение. На рисунке она обозначена розовым большим овалом.








