Разбор задачи B4 (демо ЕГЭ 2007)
Один считает, что первой будет Наташа, а Маша будет второй.
Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место.
Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.
Какое место на чемпионате заняли Наташа, Маша, Люда, Рита?
(В ответе перечислите подряд без пробелов числа, соответствующие местам девочек в указанном порядке имен.)
Обозначим предположения болельщиков как А, Б и В. Рассматрим каждое предположение от А до В. Если в предположении оба утверждения ложны или оба истинны (такого по условию задачи быть не должно), остальные предположения не рассматриваем.
Введем обозначения:
Н - Наташа, М - Маша, Л - Люда, Р -Рита.
Места будем обозначать просто цифрой.
Перепишем предположения с учетом введенных обозначений:
А) Н=1, М=2.
Б) Л=2, Р=4.
В) Р=3, Н=2.
1 способ
Построим графы для Н=1 и М=2:
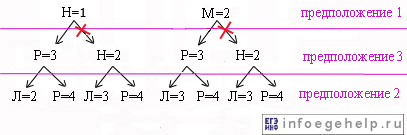
Пояснение к графам:
Пусть Н=1, тогда, учитывая предположение 3, Р=3. Ветку графа при Н=2 не учитываем (на рисунке перечеркнута красным крестом), т.к. Н=1. По 2-у предположению могли бы быть истиной или Л=2, или Р=4. Р=3, поэтому Л=2. Это ветка графа: Н=1→Р=3→Л=2.
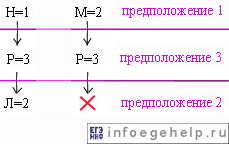
Наташа, Маша, Люда, Рита заняли места: 1423.
2 способ
Найдем, какие имена в предположениях упоминаются чаще всего. Это имена: Н (упоминается 2 раза) и Р (упоминается 2 раза).
Анализ начнем с Н. Подробно рассмотрим анализ для Н=1.
Если Н=1, то в предположении А) утверждение Н=1 - истинно. Т.к. в каждом предположении одно утверждение истинно, а другое ложно, то утверждение М=2 является ложным.
Переходим к предположению В). Здесь мы видим утверждение Н=2. Оно ложно, т.к. Н=1. Соответственно, 2-е утвержение Р=3 истинно.
Переходим к предположению Б). Здесь мы видим утверждение Р=4. Оно ложно, т.к. Р=3. Значит, 2-е утверждение Л=2 истинно.
Мы нашли решение: Н=1, Р=3, Л=2 => М=2.
Если бы решение не было найдено, мы бы проводили аналииз еще и при Н=2, Н=3, Н=4.
Для тренировки проведем этот анализ. Опишем его кратко в таблице.
Истинное утверждение выделено розовым со знаком "+", ложное - голубым со знаком "−".
| Н=1 | Н=2 |
|---|---|
|
А) Н=1+, М=2−. В) Р=3+, Н=2−. Б) Л=2+, Р=4−. |
А) Н=1−, М=2−. |
| Н=3 | Н=4 |
А) Н=1−, М=2+. В) Р=3−, Н=2−. | А) Н=1−, М=2+. В) Р=3+, Н=2−. Б) Л=2−, Р=4−. |
Получили: Н=1, Р=3, Л=2. Соответственно, М=4.
Перепишем места, как задано в условии задачи:
НМЛР=1423.
Аналогично можно было бы провести анализ для М.








