Разбор задачи B2 (демо ЕГЭ 2007)
Высказывание истинно,значит, F=1
Заменим выражения:
90<X·X=A
X < (X -1)=B
Рассмотрим таблицу истинности импликации:
| А | В | A→B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Есть 3 возможных варианта, когда импликация равна 1, т.е. A→B=1.
Решим методом от противного. Найдем такое Х, когда F=0, т.е. высказывание ложно. Поэтому должны удовлетворяться условия: А=1,В=0.
Переходим обратно к неравенствам:
(90 <X·X)=1
(X < (X−1))=0 => (X ≥ (X−1))=1
Поэтому 90<Х2 и X∈R (X может быть любое, т.к. X всегда больше, чем X−1)
Перепишем неравенства:1)Х2>90 и 2)X∈R.
Решим эту систему неравенств.
Уравнением 2) можно принебречь, поскольку пересечение какого-либо интервала со всей числовой прямой даст этот интервал.
Х2>90
Х=±√90≈±9,49
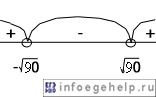
X принадлежит (-∞;-√90)U(√90;+∞)
Мы нашли решения Х для F=0. Теперь найдем Х для F=1: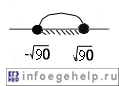
X ∈ (−√90;√90] или X ∈ (−√9,49;√9,49]
Получили, наибольшее целое Х=9.








