Разбор задачи C4 (демо ЕГЭ 2005)

Два игрока играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 4, а во второй – 3 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче или добавляет 2 камня в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 24 камней. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.

Решение:

Введем обозначения:

х - первая куча,

у - вторая куча.

Старт: (х, у).

Варианты хода игроков: (х*3,у), (х,у*3), (х+2,у), (х, у+2).

Игрок выйграет, когда число камней в 2-х кучах станет ≥24 (х+у≥24). Изобразим ход игры в виде дерева решений. Необходимо ветвить дерево до того момента, когда все варианты последнего хода станут выйгрышными.

После первого хода дерево будет выглядеть так:

Задача С4 ЕГЭ по информатике 2005 первый ход

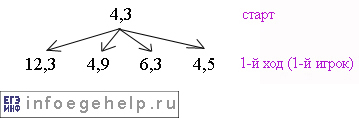
На дереве изображены все возможные варианты ходов.

После первых 2-х ходов дерево будет выглядеть так:

Задача С4 ЕГЭ по информатике 2005 второй ход

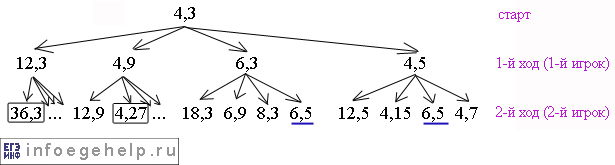
Одним цветом в строке подчертнуты одинаковые значения количества камней в кучах. По ходу игры будем ветвить только разные координаты.

Когда 2-й игрок совершает 2-й ход, он выигрывает, когда попадает в позиции: (36,3) и (4,27), т.к. сумма х и у в этих случаях больше 24. На рисунке выйгрышные позиции 2-го игрока выделены сплошной рамкой.

Мы не рассматривали остальные позиции (обозначены как "..."), если встречали выйгрышную позицию. Игроки играют безошибочно, поэтому 2-й игрок пойдет только по выйгрышной ветке. Соответственно, нет смысла рассматривать все позиции. Например, из позиции (12,3) 2-й игрок обязательно пойдет в (36,3), а не в (12,9), например.

Смотрим предыдущий ход. Чтобы 2-й игрок не выйграл, 1-й игрок на 1-м ходе не должен идти в позиции (12,3) и (4,9). Он может идти в остальные позиции. Запретные позиции для 1-го игрока перечеркнуты красным:

Задача С4 ЕГЭ по информатике 2005 запретные позиции 1-го игрока

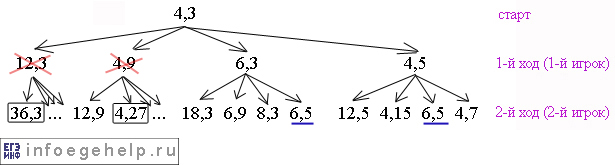
Рассматривая дальнейшие ходы не будем ветвить позиции, которые идут из позиций (12,3) и (4,9). После 3-х ходов дерево будет выглядеть так:

Задача С4 ЕГЭ по информатике 2005 третий ход

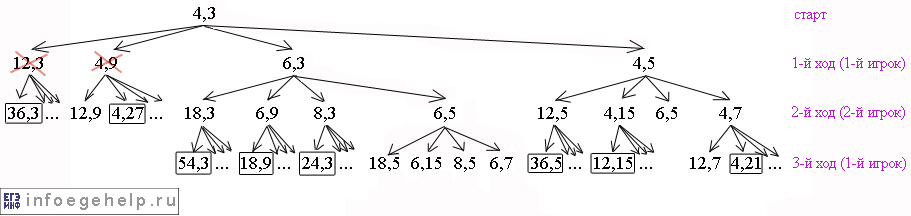
Когда 1-й игрок совершает 3-й ход, он выигрывает, когда попадает в позиции: (54,3), (18,9), (24,3) и (36,5), (12,15), (4,21) т.к. сумма х и у в этих случаях ≥24. На рисунке выйгрышные позиции 1-го игрока на 3-м ходу выделены сплошной рамкой.

Смотрим предыдущий ход. Чтобы 1-й игрок не выйграл, 2-й игрок на 2-м ходе не должен идти в позиции (18,3), (6,9), (8,3) и (12,5), (4,15), (4,7). Он может идти в остальные позиции. Запретные позиции для 2-го игрока перечеркнуты красным:

Задача С4 ЕГЭ по информатике 2005 запретные позиции 2-го игрока

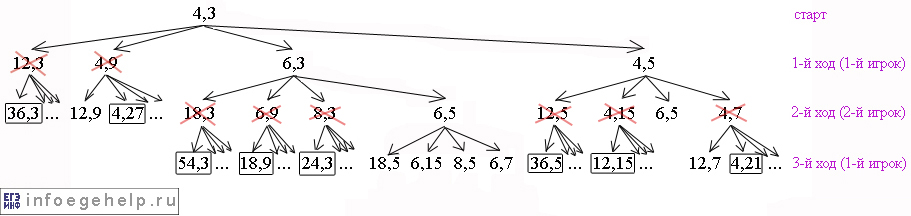
Рассматривая дальнейшие ходы не будем ветвить позиции, которые идут из позиций (18,3), (6,9), (8,3) и (12,5), (4,15), (4,7). После 4-х ходов дерево будет выглядеть так:

Задача С4 ЕГЭ по информатике 2005 четвертый ход

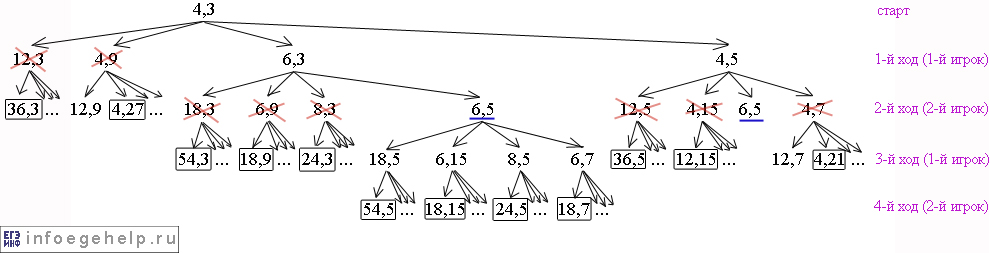
Из рисунка видно, что любой ход 2-ого игрока на 4-м ходу будет выйгрышным. Поэтому, выигрывает 2-й игрок.

Представим решение также в виде таблицы (выйгрышные ходы выделены розовым):

	1 ход	2 ход	3 ход	4 ход
Старт	1-й игрок (все ходы)	2-й игрок (выйгрышный ход)	1-й игрок (все ходы)	2-й игрок (выйгрышный ход (один из вариантов))
4,3	12,3	36,3	-	-
	4,9	4,27	-	-
	4,9	4,27	-	-
	6,3	6,5	18,5	54,5
			6,15	18,15
			8,5	24,5
			6,7	18,7
	4,5	6,5	те же ходы, что описаны выше

Выигрывает 2-й игрок.
Варианты его первого хода представлены в таблице выше, в столбце, выделенном розовым. Если 1-й игрок 1-м ходом утраивает число камней в 1-й или 2-й куче, то 2-й игрок выигрывает своим 1-м ходом, попадая в позиции: (36,3) и (4,27). При остальных ходах 1-го игрока 2-й игрок выигрывает своим 2-м ходом.

Перейти к другим задачам.

infoegehelp.ru

Разбор задачи C4 (демо ЕГЭ 2005)