Разбор задачи C4 (демо ЕГЭ 2004)
Введем обозначения:
х - количество камней в первой куче,
у - количество камней во второй куче,
z - количество камней в третьей куче.
Позиция игрока: (х, у, z).
Варианты хода игроков: (х*2,у,z), (х,у*2,z), (х,у,z*2), (х+2,у+2,z+2).
Игрок выйграет, когда
- число камней в одной из куч ≥15 (x≥15 или y≥15, или z≥15)
- число камней в 3-х кучах станет ≥25 (х+у+z≥25).
После первого хода дерево будет выглядеть так:
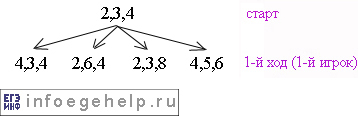
На дереве изображены все возможные варианты ходов.
После первых 2-х ходов дерево будет выглядеть так:
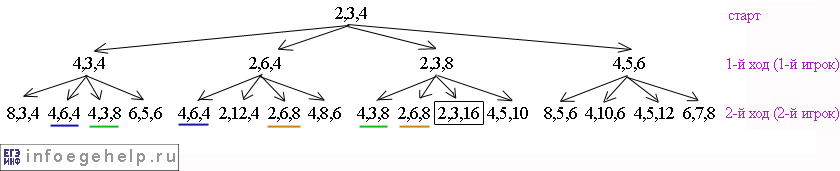
Одним цветом в строке подчертнуты одинаковые значения количества камней в кучах. По ходу игры будем ветвить только разные координаты.
Когда 2-й игрок совершает 2-й ход, он выигрывает, когда попадает в позицию: (2,3,16), т.к. z в этом случае больше 15. На рисунке выйгрышная позиция 2-го игрока выделены сплошной рамкой.
Смотрим предыдущий ход. Чтобы 2-й игрок не выйграл, 1-й игрок на 1-м ходе не должен идти в позицию (2,3,8). Он может идти в остальные позиции. Запретная позиция для 1-го игрока перечеркнута красным:
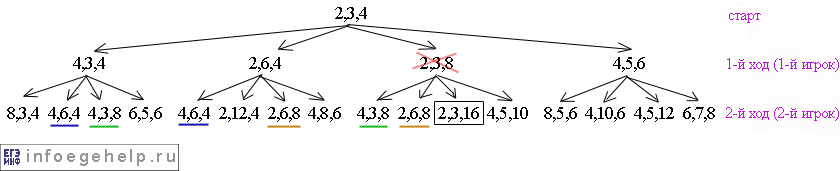
Рассматривая дальнейшие ходы не будем ветвить позиции, которые идут из позиции (2,3,8). После 3-х ходов дерево будет выглядеть так:

Для того чтобы в одной из куч стало ≥15 камней (выйгрышный ход), необходимо чтобы на предыдущем ходу в данной куче было ≥8 камней (8*2=16). Поэтому прежде чем рассчитывать все варианты хода, необходимо просмотреть все x,y,z и на наличие числа ≥8. Если такое число будет найдено, то следующий ход будет получен удвоением найденного x,y или z. Если же не будет найдено, то будут рассмотрены все возможные ходы. Например, чтобы выиграть 1-й игрок из позиции (8,3,4) обязательно пойдет в (16,3,4), а не в (8,6,4), например.
Когда 1-й игрок совершает 3-й ход, он выигрывает, когда попадает в позиции: (16,3,4), (4,3,16), (2,24,4), (2,6,16), (4,16,6), (16,5,6), (4,20,5), (4,5,24), (6,7,16), т.к. х, у или z в этих случаях ≥15. На рисунке выйгрышные позиции 1-го игрока на 3-м ходу выделены сплошной рамкой.
Смотрим предыдущий ход. Чтобы 1-й игрок не выйграл, 2-й игрок на 2-м ходе не должен идти в позиции (8,3,4), (4,3,8), (2,12,4), (2,6,8), (4,8,6), (8,5,6), (4,10,6), (4,5,12), (6,7,8). Он может идти в остальные позиции. Запретные позиции для 2-го игрока перечеркнуты красным:

Из рисунка видно, что если 1-й игрок пойдет на 1-м ходу в позицию (4,5,6) (выделено розовым), то у 2-го игрока все его возможные ходы будут запретными, т.е. приведут к выйгрышу 1-го игрока. Поэтому при правильном 1-м ходе 1-й игрок выигрывает.
Рассмотрим ситуацию, когда 1-й игрок пойдет в одну из позиций: (4,3,4) или (2,6,4).
Рассматривая дальнейшие ходы не будем ветвить позиции, которые идут из позиций (8,3,4), (4,3,8), (2,12,4), (2,6,8), (4,8,6), (8,5,6), (4,10,6), (4,5,12), (6,7,8). После 4-х ходов дерево будет выглядеть так:
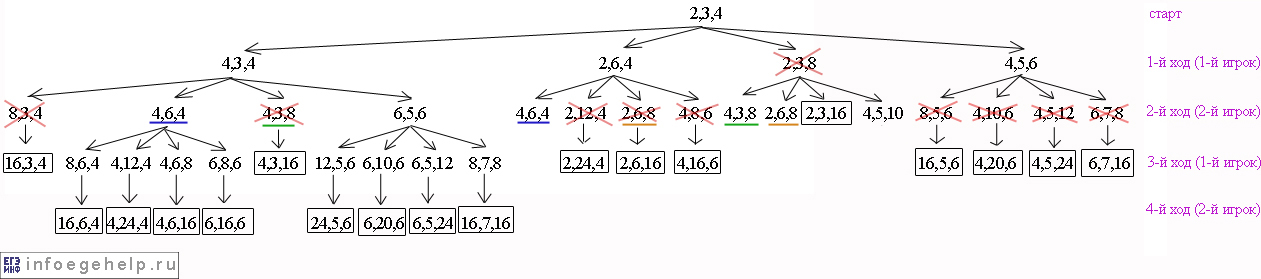
Из рисунка видно, что любой ход 2-ого игрока на 4-м ходу был бы выйгрышным при ошибочном 1-м ходе 1-го игрока.
Представим решение также в виде таблицы (выйгрышные ходы выделены розовым):
| 1 ход | 2 ход | 3 ход | |
|---|---|---|---|
| Старт | 1-й игрок (выйгрышный ход) | 2-й игрок (все ходы) | 1-й игрок (выйгрышный ход (один из вариантов)) |
| 2,3,4 |
4,5,6 |
8,5,6 |
16,5,6 |
| 4,10,6 | 4,20,6 | ||
| 4,5,12 | 4,5,24 | ||
| 6,7,8 | 6,7,16 |
Выигрывает 1-й игрок.
Вариант его первого хода представлен в таблице выше, в столбце, выделенном розовым. Если 1-й игрок 1-м ходом добавляет по 2 камня в каждую из куч, то он выигрывает своим 2-м ходом. Если он удваивает число камней в какой-либо куче, то он проигрывает. В зависимости от его хода, 2-й игрок выигрывает своим 1-м или 2-м ходом.








