 Диаграммы Эйлера-Венна
Диаграммы Эйлера-Венна
Диаграммы Эйлера-Венна
Диаграмма Эйлера-Венна - наглядное средство для работы со множествами. На этих диаграммах изображаются все возможные варианты пересечения множеств. Количество пересечений (областей) n определяется по формуле:
n=2N,
где N - количество множеств.
Таким образом, если в задаче используется два множества, то n=22=4, если три множества, то n=23=8, если четыре множества, то n=24=16. Поэтому диаграммы Эйлера-Венна используются в основном для двух или трех множеств.
Множества изображаются в виде кругов (если используется 2-3 множества) и эллипсов (если используется 4 множества), помещенных в прямоугольник (универсум).
Универсальное множество (универсум) U (в контексте задачи) - множество, содержащее все элементы рассматриваемой задачи: элементы всех множеств задачи и элементы, не входящие в них.
Пустое множество Ø (в контексте задачи) - множество, не содержащее ни одного элемента рассматриваемой задачи.
На диаграмме строят пересекающиеся множества, заключают их в универсум. Выделяют области, количество которых равно количеству пересечений.
Диаграммы Эйлера-Венна также используются для визуального представления логических операций.
Разберем примеры построения диаграмм Эйлера-Венна для двух и трех множеств.
Пример 1
Пусть есть следующие множества чисел:
А={1,2,3,4}
В={3,4,5,6}
Универсум U={0,1,2,3,4,5,6}
Диаграммы Эйлера-Венна для двух множеств А и В:
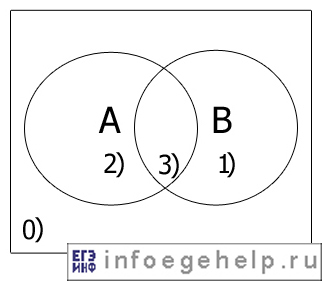
Определим области, и числа которые им принадлежат:
| А |
B |
Обозначение области | Числа |
|---|---|---|---|
| 0 |
0 |
0) | 0 |
| 0 |
1 |
1) | 5,6 |
| 1 |
0 |
2) | 1,2 |
| 1 |
1 |
3) | 3,4 |
Пример 2
Пусть есть следующие множества чисел:
А={1,2,3,4}
В={3,4,5,6}
С={1,3,6,7}
Универсум U={0,1,2,3,4,5,6,7}
Диаграммы Эйлера-Венна для трех множеств А, В, С:
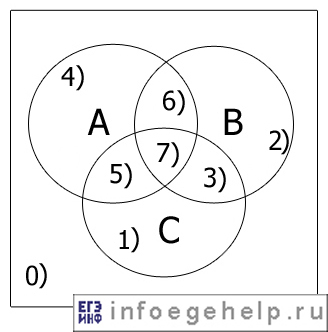
Определим области, и числа которые им принадлежат:
| А |
B |
C |
Обозначение области | Числа |
|---|---|---|---|---|
| 0 |
0 |
0 |
0) | 0 |
| 0 |
0 |
1 |
1) | 7 |
| 0 |
1 |
0 |
2) | 5 |
| 0 |
1 |
1 |
3) | 6 |
| 1 |
0 |
0 |
4) | 2 |
| 1 |
0 |
1 |
5) | 1 |
| 1 |
1 |
0 |
6) | 4 |
| 1 |
1 |
1 |
7) | 3 |
Пример 3
Пусть есть следующие множества чисел:
А={0,1,2,3,4,5,6,7}
В={3,4,5,7,8,9,10,13}
С={0,2,3,7,8,10,11,12}
D={0,3,4,6,9,10,11,14}
Универсум U={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15}
Диаграммы Эйлера-Венна для четырех множеств А, В, С, D:
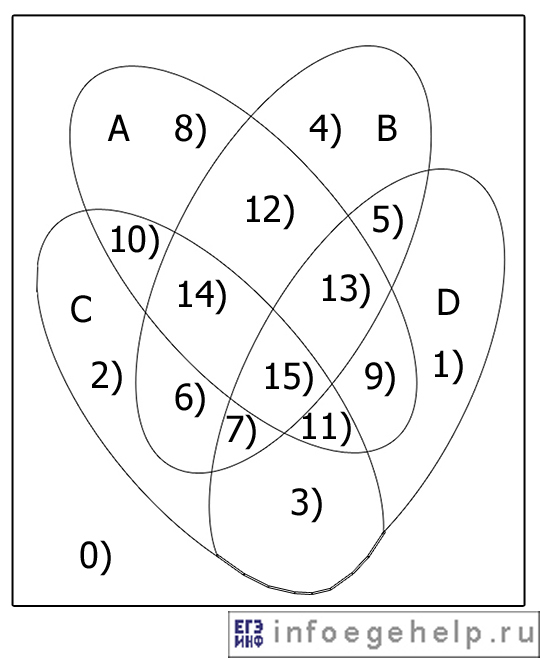
Определим области, и числа которые им принадлежат:
| А |
B |
C |
D | Обозначение области | Числа |
|---|---|---|---|---|---|
| 0 |
0 |
0 |
0 | 0) | 15 |
| 0 |
0 |
0 |
1 | 1) | 14 |
| 0 |
0 |
1 |
0 | 2) | 12 |
| 0 |
0 |
1 |
1 | 3) | 11 |
| 0 |
1 |
0 |
0 | 4) | 13 |
| 0 |
1 |
0 |
1 | 5) | 9 |
| 0 |
1 |
1 |
0 | 6) | 8 |
| 0 | 1 | 1 | 1 | 7) | 10 |
| 1 |
0 |
0 |
0 | 8) | 1 |
| 1 | 0 | 0 | 1 | 9) | 6 |
| 1 | 0 | 1 | 0 | 10) | 2 |
| 1 | 0 | 1 | 1 | 11) | 0 |
| 1 | 1 | 0 | 0 | 12) | 5 |
| 1 | 1 | 0 | 1 | 13) | 4 |
| 1 | 1 | 1 | 0 | 14) | 7 |
| 1 | 1 | 1 | 1 | 15) | 3 |
Если Вы хотите порешать типовые задач на множества, то перейдите к статье: "Как решать задачи с помощью диаграмм Эйлера-Венна". Там подробно разобрано 5 задач.
Перейти к разбору задач на множества из ЕГЭ по информатике:








