Разбор задачи A1 (демо ЕГЭ 2010)
Дано А=9D16, B=2378. Какое из чисел C, записанных в двоичной системе, отвечает условию A<C<B?
- 100110102
- 100111102
- 100111112
- 110111102
1 способ
Нужно А и В перевести в двочную систему счисления. Метод перевода числа из восьмеричной и шестнадцатеричной системы в двоичную описан в этой статье.
Сначала переведем А.Каждая цифра 16-чной системы соответствует 4 цифрам двоичной системы.
А содержит 2 цифры: 916 и D16. 9=10012.
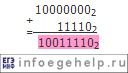
D16=1310=810+510=
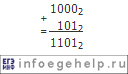
А=1001 11012
Переведем B:
Каждая цифра 8-чной системы соответствует 3 цифрам двоичной системы.
B=2378.
28=0102.
3=0112
7=1112
2378=10 011 1112=1001 1111 (для удобства сравнения разделили по четыре цифры, т.к. А представлено так)
A<C<B: 1001 11012<1001 11102<1001 11112.
2 способ
Переведем А и В в 10-чную систему счисления.
А=9D16=16*9+13=144+13=157 (D16=1310)
B=2378=2*82+3*8+7=128+24+7=159
A<C<B:157<C<159. следовательно, С=158. Переводим в двоичную систему.
158 | 2 _
14 79 | 2___
18 6 39 | 2__
18 19 2 19 | 2__
0 18 19 18 9 | 2__
1 18 1 8 4 | 2_
1 1 4 2 | 2_
0 2 1
0
Перепишем результат и все остатки: 100111102. Это искомое С.
Или можно использовать метод быстрого перевода числа из десятичной системы в двоичную, он описан в этой статье.
158=128+30.
128=100000002.
30=31-1=111112-12=111102.
158=