infoegehelp.ru

Проведем замену:

(x1 ≡ x2)=y1

(x3 ≡ x4)=y2

(x5 ≡ x6)=y3

(x7 ≡ x8)=y4

(x9 ≡ x10)=y5

Перепишем систему уравнений с учетом замены:

(y1Vy2)Λ(¬y1V¬y2)=1

(y2Vy3)Λ(¬y2V¬y3)=1

....

(y4Vy5)Λ(¬y4V¬y5)=1

Решим первое уравнение (y1Vy2)Λ(¬y1V¬y2)=1.Преобразуем логическое выражение (y1Vy2)Λ(¬y1V¬y2):

(y1Vy2)Λ(¬y1V¬y2)=(y1Λ¬y1)V(y1Λ¬y2)V(y2Λ¬y1)V(y2Λ¬y2)=0V(y1Λ¬y2)V(y2Λ¬y1)V0=(y1Λ¬y2)V(y2Λ¬y1).

Отобразим логическое выражение (y1Λ¬y2)V(y2Λ¬y1) с помощью диаграммы Эйлера-Венна:

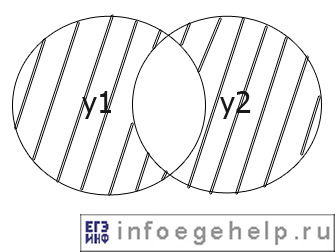
Видно по рисунку,что это инверсия эквиваленции: ¬(y1≡y2) или ¬(y1↔y2).

Перепишем уравнение: ¬(y1≡y2)=1. Отсюда (y1≡y2)=0. Такое уравнение имеет 2 решения:y1=1,y2=0 или y1=0,y2=1.

Рассмотрим 2-ое уравнение. С учетом преобразований оно становится таким:¬(y2≡y3)=1.

Решим систему из двух уравнений:

¬(y1≡y2)=1

¬(y2≡y3)=1

Перепишем систему в одно уравнение:¬(y1≡y2)Λ¬(y2≡y3)=1.

Преобразуем ¬(y1≡y2)Λ¬(y2≡y3):

¬(y1≡y2)Λ¬(y2≡y3)=¬( (y1≡y2)V(y2≡y3) )-выносим отрицание за скобки.

Уравнение примет вид:¬( (y1≡y2)V(y2≡y3) )=1. Отсюда (y1≡y2)V(y2≡y3)=0.

Логическое выражение выполняется, только когда (y1≡y2)=0 и (y2≡y3)=0.

Пусть y2=0.

y1≡0=0-выполняется при y1=1.

0≡y3=0-выполняется при y3=1.

Получаем одно решение:y2=0,y1=1,y3=1.

Пусть y2=1.

y1≡1=0-выполняется при y1=0.

0≡y3=0-выполняется при y3=0.

Получаем одно решение:y2=1,y1=0,y3=0.

Общее число решений при двух уравнениях системы:1+1=2 решения.

Таким образом,при добавлении одного уравнения к самому первому уравнению не меняется число решений, остается равным двум. Следовательно, добавление остальных уравнений не изменит общее количество решений. Остается два решения.

Теперь перейдем к поиску количества решений, используя обратную подстановку для y.

y1=(x1 ≡ x2)-для каждого из значений y1 есть два решения. Например,если y=0,то x1=0,x2=1 или x1=1,x2=0.

y2=(x3 ≡ x4)-для каждого из значений y2 есть два решения.

Аналогично и для остальных:y3,y4,y5. Пары решений (x1,x2),(x3,x4),(x5,x6),(x7,x8),(x9,x10) - не зависят друг от друга, поэтому комбинаций решений равно 2⁵=32.(основание равно 2,т.к. каждая пара дает два решения, а степень равна 5,т.к. у нас есть 5 пар).

В данном случае мы не учли, что и y1,y2,y3,y4,y5 дают нам в два раза больше решений.

Общее количество решений:32*2=64 решения.